주의 : 잘못된 내용이 포함되어 있을 수 있으므로 이상하면 참고자료를 확인하세요.
[ PBR 이란 무엇인가 ] 21. PBR Shader 구성
챕터 20 까지 하고 글을 마무리하려고 했는데, 궁금해 하시는 분이 계셔서 글을 추가합니다.
아마도 프로그래머나 TA 라면 PBR 을 실제로 어떻게 구성해야 하는지에 대한 의문이 들 겁니다.
각각의 의미는 알겠는데 셰이더의 결과에는 무엇이 반영되어야 하나요?
우리는 [ 9. Global Illumination & Indirect Lighting ] 에서 조명은 Direction Lighting 과 Indirect Lighting 으로 구분된다는 것을 알게 되었습니다. 이러한 조명들 중에서 눈에 도달하게 되는 성분들이 셰이더 계산의 결과가 됩니다.
조명 분석
눈에 들어 오는 빛들을 정리해 보죠. 여기에서는 대기 산란( atmospheric scattering )과 같은 복잡한 현상에 대해서는 언급하지 않고 기본적인 것들에 대해서만 다루도록 하겠습니다. 그림 1 에 눈에 들어 오는 빛의 몇 가지 샘플들을 그려 봤습니다.
그림 1.
여러분은 그림 1 에 있는 빛들의 카테고리를 규정할 수 있어야 합니다. 반사나 굴절을 통해 눈으로 직접 들어 온 빛은 직접 조명( direct lighting )이며, 다른 물체에 튕겨졌다가 온 빛은 간접 조명( indirect lighting )입니다.
- 1 : [ direct ] diffuse + specular.
- 2 : [ direct ] diffuse + specular.
- 3 : [ direct ] emissive( 방출 ). 물체 자체가 발광하고 있음.
- 4 : [ indirect ] diffuse + specular.
- 5 : [ direct ] diffuse + specular.
- 6 : [ direct ] diffuse + specular.
- 7 : [ indirect ] transmission( 투과 ).
- 8 : [ indirect ] diffuse + specular.
- 9 : [ direct ] transmission.
여기에서 혼란에 빠지는 분들이 있을 겁니다.
제 눈에는 정반사 성분은 안 보이는데요, 왜 "diffuse + specular" 가 들어 오는 건가요?
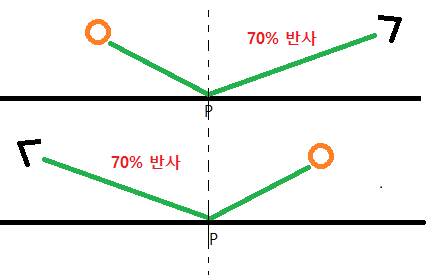
스펙큘러 반사는 정반사( 입사각과 반사각이 동일한 반사 )만을 의미하는 것이 아닙니다. 특정 방향을 중심으로 로브( lobe )를 형성합니다. 스펙큘러 반사가 얼마나 퍼지냐는 BRDF 에 의해서 결정되죠. 이것은 표면이 완전히 평평하지 않기 때문에 발생하는 현상입니다. 그림 2 에서 여러 형태의 로브를 보여 주고 있습니다.
그림 2. 매질의 거칠기에 따른 스펙큘러 로브. 출처 : [Specular IBL].
그러므로 정반사 각도가 아니더라도 스펙큘러가 눈에 들어 올 수 있는 것입니다.
자, 이제 눈에 들어 올 수 있는 빛의 성분들을 나눠 보죠. 빛이라는 것은 눈에 들어 오면 누적되기 때문에 다음과 같은 식을 세울 수 있습니다.
식 1.
식 1 이 기본적인 셰이더의 함수입니다.
간단하게 머리글자로 표기하도록 하겠습니다.
식 2.
그런데 식 2 를 보고 있으면 의문이 생길 겁니다. 셰이더라는 것이 화면상의 한 픽셀에 대해서 처리됩니다. 그런데 어떻게 여러 광원에서 오는 빛을 처리할 수 있을까요?
그래서 실제로 결과는 다음과 같이 처리되어야 합니다.
식 3.
식 3 에서 Sigma 연산자는 괄호 안의 요소를 모두 더한 결과를 누적한다는 의미입니다. 광원이 1 부터 n 까지 있을 때 각각의 diffuse, specular, transmission 를 더한 결과를 모두 누적한다는 겁니다.
여기에서 하나의 의문을 가질 수 있습니다.
왜 E 는 광원별로 처리하지 않나요?
방출( Emissive ) 은 광원에서 발생하는게 아니라 재질의 특성입니다. 그러므로 한 번만 처리됩니다.
이런 계산을 셰이더에서 수행하는 방법은 여러가지가 있는데, 크게 두 가지 방식으로 처리됩니다. 여기에서는 누적된 광원을 적용하는 패스가 따로 있다는 가정을 가지고 있습니다.
- 한 셰이더에서 한 개의 광원에 대한 결과를 처리하고 광원을 바꿔가면서 여러 패스를 실행할 수 있습니다.
- 한 셰이더에서 여러 개의 광원의 결과를 한꺼번에 처리합니다.
그림 3. 조명 누적.
그런데 사실 싱글패스를 구현하는 것은 어렵습니다. 셰이더라는 것이 화면의 전체 픽셀에 대해서 적용되므로 불필요한 계산이 수행될 수 있습니다. 게다가 몇 개의 광원을 처리해야 할지 애매하죠. 셰이더에서 무거운( 지금은 안 무거울라나... ) 루프를 돌려야 합니다. 그래서 최적화를 위해서 광원 영역에 대한 stencil 을 찍어 두거나 영역( viewport, scissor-rect )을 따로 잡은 후에 멀티패스로 돌리는 경우가 많습니다.
Direct Lighting vs Indirect Lighting
눈썰미가 좋은 분들은 식 3 에 직접 광원 성분과 간접 광원 성분이 분리되어 있지 않다는 것을 눈치채셨을 겁니다.
간접 광원은 매우 계산하기 힘들기 때문에 보통은 라이트맵( Lightmap )을 사용하거나 IBL( Image-Based Lighting ) 큐브맵을 사용하게 됩니다. 라이트맵과 IBL 큐브맵에 대해서 여기에서 자세하게 설명하지는 않겠습니다. 검색해 보면 관련 자료들이 많으니 그것들을 참고하시기 바랍니다.
여기에서는 그것들의 차이만을 간략하게 설명하도록 하겠습니다. 나중에 기회가 되면 한 번 정리하도록 하겠습니다.
- 라이트맵은 정적인 라이팅 환경을 대상으로 구워집니다. 그래서 일반적으로 어느 방향에서 봐도 동일한( 뷰 독립적인, view-independent ) 디퓨즈 성분만을 저장합니다. 일반적인 라이트맵을 사용하게 되면 스펙큘러 성분을 알 수 없습니다. 대신 스펙큘러 성분을 어느정도 반영하기 위해서 RNM( Radiosity Normal Map ) 라이트맵이라는 것이 있기는 하지만 이것 역시 정적 환경이라는 점에서는 차이가 없습니다.
- IBL 큐브맵은 조도( irradiance ) 샘플을 저장합니다. 어떤 기준점을 중심으로 주변의 빛들을 모두 광원으로 처리합니다. 여기에는 디퓨즈 성분과 스펙큘러 성분이 모두 들어 갈 수 있습니다. 실시간에 큐브맵을 생성한다면 동적인 라이팅 환경을 반영하는 것도 가능합니다( 물론 성능 저하는 감수해야 합니다. 큐브맵을 다시 만들어야 하기 때문이죠 ). 동적인 라이팅을 허용하는 IBL 구현은 현재 많지 않습니다. 기존에 Asker 라는 게임 프로젝트에서 프레임별로 각 면을 나눠서 생성한 적은 있는데, 그것만으로도 큰 부하가 듭니다. 단순하게 씬을 렌더링하는 것을 떠나서 임포턴스 샘플링( importance sampling )같은 것도 해야 하기 때문입니다. 게다가 시차때문에 생기는 문제를 해결( 시차 보정, Parallax Correction )해야 합니다. 현재 하드웨어에서는 사용할만 한지는 잘 모르겠네요. 펄 어비스에 다니는 지인의 말로는 실제로 프로젝트에서 사용하고 있다고 하는 것 같더군요. 이 외에도 여러 가지 문제( 캡쳐 범위 등 )가 존재하는데 잡다한 문제를 다 해결해야지 사용할 만 합니다.
어쨌든 라이트맵이나 IBL 큐브맵을 사용해서 간접광 성분을 계산할 수 있습니다.
그러므로 식 3 은 다음과 같이 변경됩니다.
식 4.
"dl" 은 직접광을 의미하며 "il" 은 간접광을 의미합니다.
그런데 사실 투과( Transmission )같은 경우에는 서브 서피스 스캐터링( Sub-Surface Scattering )이 아니라면 일반적으로는 배제합니다. 피부나 초같은 밀랍( Wax )같은 재질이 아니라면 그냥 투과는 처리하지 않습니다. 왜냐하면 그 비용이 상당히 비싸기 때문이죠. 하지만 어쨌든 일반식을 만드는 것이니 식은 그냥 두겠습니다.
에너지 보존 법칙
마지막으로 고려해야 할 부분은 에너지 보존법칙입니다.
일반적으로 에너지 보존법칙은 디퓨즈와 스펙큘러에만 적용합니다. Emissive( 방출 )은 자체적으로 에너지가 생성된 것이고 에너지 보존 법칙이 성립하려면 다음과 같이 되어야 합니다.
식 5.
그런데 일반적인 BRDF 식에서의 Diffuse, Specular, Transmission 에는 이미 Absorbtion( 흡수 ) 이 포함되어 있습니다. 이런 계산까지 전부 다 하게 되면 엄청나게 복잡해질 겁니다. 물론 이런 계산을 포함한 BRDF 도 어딘가에는 있겠죠. 제가 BRDF 함수들을 모두 완벽하게 알고 있는 게 아니라서 잘은 모르겠습니다.
그러므로 일반적으로는 Diffuse 와 Specular 에 대해서만 에너지 보존 법칙을 적용하게 됩니다. 그게 눈에 가장 잘 보이기 때문입니다.
보통 Specular 의 세기는 금속성( metalic )에 의해서 결정되고 있기 때문에 metalic 을 에너지 보존법칙을 적용하는데 사용합니다. 물론 구현마다 차이는 있을 수 있습니다만, 적어도 UE4 는 metalic 을 기준으로 사용합니다.
그래서 식 4 에 에너지 보존 법칙을 적용하면 다음과 같습니다.
식 6.
BRDF 와 Light Intensity
가끔 BRDF 식을 보면 Light Intensity 를 포함하고 있는 경우가 있습니다. 챕터 20 댓글에 어떤 분이 이와 관련한 질문을 하셨습니다. 요약하자면 "Light Intensity 와 BRDF 의 관계가 어떻냐"는 것이었습니다.
그분이 예로 드신 Oren-Nayar BRDF 식은 다음과 같습니다.
식 7. Oren-Nayar BRDF. 출처 : [ Oren-Nayar reflectance model ], Wikipedia.
해당 문서에서는 E0 를 미세면에 도달한 조도( E0 is irradiance when the facet is illuminated head-on )라고 이야기하고 있습니다. 그리고 Lr 을 휘도( the radiance of the reflected light Lr ) 라고 이야기하고 있습니다. E0 이 일반적으로 Light Intensity 라 할 수 있습니다.
여기에서 두 가지 이슈가 발생합니다.
- Light Intensity 에는 어떤 값이 들어 가야 하나요?
- 식 7 에다가 Light Intensity 를 곱해야 하는 것일까요?
첫 번째 질문에 대해서 이야기하자면, 일단 대부분의 BRDF 함수들은 Light Intensity 로 칸델라( Candela, cd )를 받는 것으로 알고 있습니다. 위에서도 미세면에 도달한 빛( 조도 )에 대한 함수이기 때문에 이것은 칸델라여야 합니다. 칸델라는 단위 입체각당 광속을 의미합니다. UE4 에서는 점광원에 대해서 광속( luminous flux, lm )을 받다가 최근에 칸델라를 받도록 수정했죠. 광속이 뭔지 기억이 안 나시는 분들은 [ 4. 광원의 밝기( 광속 ) ] 챕터를 참조하시기 바랍니다.
두 번째 질문에 대해 답하자면, Light Intensity 가 BRDF 공식에 이미 적용되어 있다면 적용하지 말아야 한다는 겁니다. 그러므로 BRDF 셰이더 함수를 만든다면 Light Intensity 가 배제된 순수한 BRDF 를 만드는 것이 좋겠죠. 식 7 의 경우에는 E0 을 배제한 나머지 항들이 순수한 BRDF 식의 항들입니다.
정리
기본적으로 그래픽스에서 휘도( radiance, luminance )를 다룰 때는 눈에 들어 오는 모든 빛은 누적된다고 생각해야 합니다.
단지 해당 빛이 어디에서 오는지를 명확하게 할 필요가 있습니다. 그래야지 조명별로 처리할지 한 번만 처리할지 결정할 수 있기 때문입니다.
하지만 더하기만 하지는 않는 경우도 존재합니다. 예를 들어 차폐같은 것들이 그렇죠. 하지만 차폐도 보통 빛을 아예 누적하지 않거나 감쇠( attenuation ) 비율을 곱하는 식으로 적용하는 경우가 많습니다. Ray-Tracing 기법을 사용하면 무조건 더하기만 해도 아무 문제가 없지만 Rasterization 에서는 이런 저런 꼼수들이 들어 갑니다. 여기에 대해서 자세하게 언급은 안 하겠지만, Ray-Tracing 과 Rasterization 의 차이에 대해서 한 번 찾아 보는 것도 생각을 정리하는데 많은 도움이 될 것이라 생각합니다.
나름대로 정리한다고 하긴 했지만 빠져 있는 성분들이 꽤 많습니다; 대기산란, 차폐( Shadow, Ambient Occlusion 등 ).
하지만 BRDF 공식을 가지고 있을 때 어떻게 이것들을 결합해야 할지에 대해서는 대충 감이 오셨을 것이라 생각합니다.
PS : 반투명 재질을 렌더링한 결과( 우리가 일반적으로 사용하는 알파블렌딩 )는 투과( Transmission ) 성분을 반영합니다. 단지 IOR( Index Of Reflection )을 고려하지 않아서 굴절( Refraction )이 없는 것처럼 보일 뿐입니다. 투과 성분은 광원에서의 빛이 매질 내부에서 산란이 된 후 튀어 나오는 성분이기 때문에 매우 계산이 어렵습니다. 그래서 보통 후처리( Post-Process ) 패스에서 대충 왜곡( distortion )하는 식으로 처리합니다.
'PBR(Physically Based Rendering)' 카테고리의 다른 글
| [ PBR 이란 무엇인가 ] 20. Specular BRDF (27) | 2017.10.22 |
|---|---|
| [ PBR 이란 무엇인가 ] 19. Diffuse BRDF (2) | 2017.10.15 |
| [ PBR 이란 무엇인가 ] 18. Distribution Function (4) | 2017.10.09 |
| [ PBR 이란 무엇인가 ] 17. Fresnel 이란? (12) | 2017.09.17 |
| [ PBR 이란 무엇인가 ] 16. Reflection 에 대한 잘못된 상식들 (2) | 2017.09.10 |
| [ PBR 이란 무엇인가 ] 15. [ 번역 ] 모든 것은 프레넬을 가집니다 (2) | 2017.09.03 |
| [ PBR 이란 무엇인가 ] 14. [ 번역 ] 모든 것은 빛납니다 (0) | 2017.09.03 |
| [ PBR 이란 무엇인가 ] 13. UE4 GI : Lightmass & Mobility (2) | 2017.08.27 |
| [ PBR 이란 무엇인가 ] 12. UE4 GI : Reflection Capture (6) | 2017.08.20 |
| [ PBR 이란 무엇인가 ] 11. UE4 GI : Sky Light (4) | 2017.08.01 |




























































 IOR_Table.pdf
IOR_Table.pdf




















































































































































































