주의 : 잘못된 내용이 포함되어 있을 수 있으므로 이상하면 참고자료를 확인하세요.
[ PBR 이란 무엇인가 ] 18. Distribution Function
그래픽스에 익숙하신 분들이라면 BSDF, BRDF, BTDF 와 같은 용어들을 한 번쯤은 보셨을 겁니다. 뭔진 잘 모르겠지만 DF 라는 머릿글자가 동일하다는 것을 알 수 있습니다. 제목에서 이야기하고 있는 "Distribution Function" 의 머리글자가 바로 "DF" 입니다. "Distribution Function" 은 우리말로는 "분포 함수" 정도로 표현할 수 있습니다.
우리는 여러 3D 저작 도구들에서 BRDF 라는 용어를 볼 수 있습니다.
그림1. 3DS Max 의 BRDF 롤아웃.
그림2. Maya 의 Specular 패널.
그림3. V-RAY for Maya 의 Reflection 패널.
그림4. Anorld for Maya 의 Specular 패널. 여기에서는 "Microfacet Distribution" 이라고 되어 있는데 이것도 BRDF 입니다.
명식적으로 BRDF 라는 용어를 사용하지 않더라도 BRDF 관련 파라미터들을 사용하는 경우가 많습니다. 여러분에게 익숙한 "Glossiness" 라든가 "Specular Power" 같은 용어들을 보셨을 겁니다. 보통 그것은 "Phong" 혹은 "Blinn Phong" 을 위한 BRDF 파라미터죠.
딱히 BRDF 에 대해서 알지 못한다고 하더라도 여러 가지 쉐이딩 모델을 비교하는 글들을 본 적이 있었을 겁니다( 그림5 참조 ).
그림5. BRDF 비교. 출처 : Experimental Analysis of BRDF Models.
이런 쉐이딩 모델들의 차이는 어디에서 발생하는 것일까요? "답정너" 같지만 바로 분포 함수( Distribution Function )의 차이입니다.
함수란?
함수라는 것은 무엇입니까? 그것은 입력이 들어 오면 출력을 내뱉어 주는 기계상자로 비유할 수 있습니다.
그림6. 함수를 기계에 비유함. 출처 : [ 2 ].
그림6 에서 볼 수 있듯이 "x" 라는 입력을 넣을 때 "f(x)" 라는 출력을 줍니다. "f" 는 "function" 의 머리글자입니다. 이때 x 의 값이 될 수 있는 값들의 집합을 정의역이라 하고, f(x) 의 값이 될 수 있는 값들의 집합을 치역이라고 합니다.
그런데 여기에서 제약이 있습니다. 반드시 x 와 f(x) 의 값은 1:1 로 대응해야만 한다는 것입니다. 만약 1:1 로 대응하지 않으면 어떤 일이 발생할까요? 여러분이 쿠킹머신에 재료 "A" 를 넣었는데 음식이 "B" 일 수도 있고 "C" 일 수도 있습니다. 이것을 의도한 것이 아니라고 한다면, 이러한 기계를 신뢰할 수 있을까요?
그래서 x 와 f(x) 의 값은 반드시 1:1 로 대응해야 수학적으로 올바른 함수라고 할 수 있습니다. 이 때 이런 f(x) 값들만 모아 놓은 것을 공역이라고 합니다. 그러므로 공역은 치역의 부분집합이죠( 그림 7 참조 ).
그림7. 정의역, 치역, 공역의 관계. X( 붉은색 ) 는 정의역, Y( 파란색 ) 는 치역, 노란색은 공역.
자 이제 "분포 함수" 에서 함수의 의미를 아시겠죠? 특정 입력에 대해서 특정 결과를 내 주는 것이 바로 함수입니다.
함수 f 가 있고 그것은 "f(x) = x + 1" 라고 정의되었다고 합시다. 그러면 반드시 "f(1) = 2" 여야합니다. "f(1) = 3" 일 수도 있고 "f(1) = -1" 일 수도 있으면 안 되겠죠?
그런데 세상에 안 되는 것이 어디있겠습니까? 음함수( Implicit Function ) 이라는 개념이 있습니다. 대표적인 음함수는 원이죠.
식1. 원을 위한 음함수.
이것을 그래프로 그리면 어떻게 될까요?
그림8. 원의 그래프.
식1 을 보시면 알겠지만 하나의 x 값에 두 개의 y 값이 대응됩니다. 그래서 이를 함수로 만들 수가 없죠. 그러므로 이것을 두 개의 함수( explicit function )로 나눠서 그리게 됩니다( 원을 하나의 함수로 그리는 방법이 있긴 합니다. 바로 매개변수를 도입하는 방법인데요, 이것에 대해서는 나중에 기회가 되면 설명하도록 하겠습니다 ).
어쨌든 중요한 것은 어떤 식의 입력값과 출력값이 반드시 1:1 로 대응해야만 그 식을 함수라고 부를 수 있다는 것입니다.
분포란?
"분포"라는 것은 무엇일까요? 확률이나 통계에서 많이 나오죠? 분포는 어떤 요소들이 일정한 범위에 퍼져 있는 모양을 의미합니다. 이것을 함수로 나타내면 분포함수가 되겠죠.
그림9. 정규분포 그래프. 출처 [ 3 ].
그림10. 주사위 두개를 던질 때의 두 눈의 합 S 에 대한 확률분포. 출처 : [ 3 ].
분포라는 것은 어렵게 생각할 필요가 없습니다. 그냥 어떤 패턴이라고 생각하시면 됩니다. 사실 그래픽스에서의 분포는 해석학 영역에 속하기 때문에 조금 다른 의미를 가지고 있지만, 그냥 "분포는 패턴" 이라고 이해하시는 것이 좋습니다( 여기에서 디랙델타함수[ 4 ]를 다룸으로써 미적분과 양자론에 대해 이야기하고 싶지는 않군요 ㅠㅠ ).
그래픽스에서 분포는 그림11 과 같이 로브( lobe )로 표현되는 경우가 많습니다. 로브라는 것은 어떤 물체의 둥글거나 평평한 부분을 일컽는 말입니다. 쉐이더의 차이점이 궁금해서 검색을 해 본 경험이 있는 분들은 그림11 과 같은 그림을 보신 적이 있을 겁니다.
그림11. 여러 reflection lobe 들에 대한 표현. 출처 : Explain the shape of a specular lobe.
위의 그림을 어떤 식으로 이해해야 하는지 알아 볼까요? 그림12 에는 붉은색으로 A, B, C 가 있습니다. 이것은 관찰자의 위치를 나타내는 것이죠. 일단 다른 것은 놔두고 "Standard Phong specular lobe" 에 대해서만 알아봅시다( 녹색 로브 ). 원점을 O 라 할 때 OA, OB, OC 가 녹색로브와 만나게 될때까지의 길이가 바로 specular 의 세기를 의미합니다. OA 와 OB 를 비교해 보면 녹색로브와 만날 때까지의 길이는 OB 쪽이 더 길다는 것을 알 수 있습니다. 이는 관찰자가 A 에 있을 때보다 B 에 있을 때 specular 를 더 세게 받는다는 것을 의미하죠. OC 같은 경우에는 녹색 로브와 만나지를 않는군요. 결국 specular 세기는 0 이라는 의미입니다.
그림12. Lobe 와 관찰자 A, B, C 의 관계.
여러분은 specular lobe 의 모양만 보고도 specular 가 뾰족하게 보일지 퍼져 보일지를 알 수 있습니다.
컴퓨터 그래픽스와 PBR 의 선구자인 Disney 같은 경우에는 툴까지 만들어서 BRDF 를 연구하더군요. BRDF Explorer 라는 툴이 있습니다. 링크에 가면 받을 수 있습니다. 그림13 처럼 2D 와 3D 에서 로브를 확인하거나 할 수가 있습니다. 실제로 BRDF 모델을 만들 수도 있습니다.
어떤 쉐이더를 만들기 전에는 BRDF Explorer 를 통해서 아티스트와 그 결과를 미리 확인해 보는 것도 좋겠죠.
그림13. Disney BRDF Explorer 스크린샷. 출처 : BRDF Explorer.
BRDF 와 BTDF
예전에 [ 6. 휘도 측정 ] 에서 BRDF, BTDF 그림을 보여 준 적이 있습니다.
<p
그림14. BRDF 와 BTDF. 출처 : [ 1 ]
반사되서 나가는 빛의 분포를 다루는 것이 RDF( Reflectance Distribution Function, 반사율 분포 함수 ) 이고 투과되서 나가는 빛의 분포를 다루는 것이 TDF( Transmittance Distribution Function, 투과율 분포 함수 ) 입니다.
쉽게 이야기하면 표면에 들어 온 빛이 얼마만큼 반사되었고 얼마만큼 투과되었느냐를 함수로 나타낸 것이죠. 물론 반사는 diffuse 와 specular 가 존재하기 때문에 Diffuse RDF 와 Specular RDF 로 나뉩니다.
자 우리가 자주 접하는 분산함수들은 앞에 "B" 가 붙었죠? 이것은 "Bidirectional" 의 머리글자입니다. 이게 무슨 말이냐? 그림15 처럼 빛과 관찰자의 위치가 변경되어도 관계만 같으면 결과( 반사율 혹은 투과율 )가 동일하다는 것입니다. 반사로 치면 입사각과 반사각이 같으면 어디에 있어도 반드시 같은 결과가 나온다는 의미입니다.
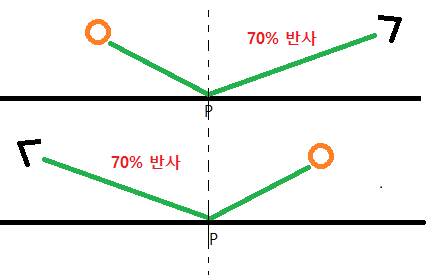
그림15. Bidirectional 의 의미. 입사각과 반사각의 관계가 동일하면 항상 동일한 결과가 나옴.
그런데 왜 bidirectional 이 필요할까요? 여기에 대해서는 명확하게 정리된 글이 없더군요. 그냥 제 생각을 말씀드리도록 하겠습니다.
컴퓨터 그래픽스에서는 성능( 혹은 속도 )을 상당히 중요한 요소로 보고 있습니다. 특히나 실시간 그래픽스라면 그것의 중요도는 말할 필요도 없겠죠. 만약 관찰자와 광원의 관계에 의해 일정한 결과를 도출할 수 없다면, 매우 복잡한 공식이 필요할 겁니다. 예를 들어 그림16처럼 서피스에 방향성이 있는 결이 있다고 하죠.
그림16. 서피스의 방향성 있는 미세한 결.
그림16 와 같은 서피스를 고려한다면 그림15 와 같은 결과를 기대할 수 있을까요? 사용자가 원하는 결과를 얻을 수는 있겠지만 재질이나 기하학적 위치에 따라 공식이 틀려져야 할 것입니다. 아티스트가 이런 것을 모두 관리하기도 힘들 뿐더러 공식이 복잡해지면서 성능도 저하되겠죠.
물론 PBR 에서는 눈에 거의 보이지 않는 미세면( microfacet )이라는 것을 고려하기는 하지만 그림16 처럼 특정 방향성으로 쏠려 있는 미세면이 아닙니다. 일정한 분포를 가지고 있는 미세면들입니다. 그것을 "Microfacet Model" 이라고 부릅니다. 이것에 대해서는 나중에 다루도록 하겠습니다.
어쨌든 일정한 분포를 가진 미세면들을 고려하면 빛과 관찰자의 관계에 의한 반사율은 일관된 방식으로 정의됩니다. 즉 bidirectional 한 성격을 띄게 되며, 하나의 재질에 대해 빛과 관찰자의 관계에 따른 여러 가지 공식을 가지고 있을 필요가 없겠죠.
P.S. "그렇다면 BRDF 로 방향성을 가진 결을 만들 수는 없나요?" 라는 질문을 하실 수 있습니다. 안 되는 게 어디 있겠습니까? NormalMap 등을 사용해서 Normal 을 왜곡시킴으로써 결을 만들어낼 수 있습니다. 하지만 이것은 관찰자와 빛의 관계에 의해 일관된 결과가 나온다는 대전제를 깨는 것은 아닙니다.
참고자료
[ 1 ] Bidirectional scattering distribution function, Wikipedia.
[ 2 ] 함수, 위키백과.
[ 3 ] 확률분포, 위키백과.
[ 4 ] 분포 (해석학), 위키백과.
'PBR(Physically Based Rendering)' 카테고리의 다른 글
| [ PBR 이란 무엇인가 ] 21. PBR Shader 구성 (22) | 2019.08.03 |
|---|---|
| [ PBR 이란 무엇인가 ] 20. Specular BRDF (27) | 2017.10.22 |
| [ PBR 이란 무엇인가 ] 19. Diffuse BRDF (2) | 2017.10.15 |
| [ PBR 이란 무엇인가 ] 17. Fresnel 이란? (12) | 2017.09.17 |
| [ PBR 이란 무엇인가 ] 16. Reflection 에 대한 잘못된 상식들 (2) | 2017.09.10 |
| [ PBR 이란 무엇인가 ] 15. [ 번역 ] 모든 것은 프레넬을 가집니다 (2) | 2017.09.03 |
| [ PBR 이란 무엇인가 ] 14. [ 번역 ] 모든 것은 빛납니다 (0) | 2017.09.03 |
| [ PBR 이란 무엇인가 ] 13. UE4 GI : Lightmass & Mobility (2) | 2017.08.27 |
| [ PBR 이란 무엇인가 ] 12. UE4 GI : Reflection Capture (6) | 2017.08.20 |
| [ PBR 이란 무엇인가 ] 11. UE4 GI : Sky Light (4) | 2017.08.01 |















