주의 : 이 문서는 책의 요약본이 아닙니다. 책을 보다가 이해가 잘 안 되는 내용, 재밌었던 내용, 보충해야 할 만한 내용 등을 정리해 놓은 일종의 노트같은 것입니다. 개인적으로는 정기적이고 의미있게 책을 보려는 시도이며, 이 책을 보는 다른 사람에게도 도움이 되었으면 좋겠습니다.
[ 이야기로 아주 쉽게 배우는 삼각함수 ] 5. 호도법( 라디안 각도 ).
드디어 고블린의 부하가 등장한다. 이 장은 제목과는 다르게 단순하게 호도법 뿐만 아니라 여함수에 대한 담고 있다.
원문 표기.
라디안( 호도 ) : radian.
중심각 : central angle.
동위각 : a corresponding angle.
변역 : codomain.
호도법의 발견.
로봇인 팔에게 총을 "1 m 회전시켜" 라고 명령하는데서 "회전의 길이" 라는 개념을 생각하고 다시 "회전 각" 이라는 개념을 생각하는 과정을 보여 준다. 그런데 이야기가 좀 억지스럽다.
만약 내가 저자였다면 "팔의 팔과 총의 길이가 달라지면 1m 회전시키라고 했을 때 쏘는 방향이 달라지는 데 이걸 어떻게 하죠?" 라는 질문에서 글을 시작했을 것 같다. 그래야 뭔가를 회전시킬때 길이 보다는 각도를 사용해야 하는 것의 필요성을 강조할 수 있었을 것 같다.
그림 1. 회전 반경과 쏘는 방향의 차이.
원의 좌표, 삼각함수, parametric equation.
이전에도 언급했던 거지만, 삼각함수는 원과 연관지어 생각하는 것이 더 좋은 것 같다. 실제로 3D 관련 업무를 하다가 보면 그런 관점이 많이 필요한 것 같다. 특히 parametric function 의 경우에 이런 관점은 중요하다.
책에 나와 있듯이 원의 정의와 피타고라스 정리로부터 다음과 같은 식을 유도할 수 있다.
그림 2. 원과 피타고라스 정리.
하지만 위의 공식으로는 "x, y, r 중 두 값을 알고 있을 때, 나머지 한 항의 값을 구하라" 라는 식의 문제만 풀 수 있지 실제 응용프로그램에서는 사용하기 힘들다. 왜냐하면, 예를 들어 r 만 알고 있을 때 ( x, y ) 의 해는 무한하게 많이 존재하기 때문이다. 게다가 r 과 x 를 알고 있다고 해도 y 의 해는 두 개가 나오게 된다( 양수와 음수 ).
그렇다면 r 을 알고 있을 때, 어떻게 원을 그릴 수 있을까? 이럴 때는 parametric equation 을 사용할 수 있다. Wikipedia 에는 다음과 같이 정의되어 있다.
수학에서, curve 의 parametric equation 은 curve 의 한 점의 좌표를 parameter 라는 변수로서 표현하는 공식을 통해 이 curve 를 표현하는 한 방법이다. 예를 들어,
는 단위 원에 대한 parametric equation 이다. 여기에서 t 가 parameter 이다.
- 출처 : Parametric equation. Wikipedia.
다시 말해 다음과 같은 식으로 curve( 여기에서는 원 ) 상의 한 점을 parametric equation 으로 표현할 수 있다.
그림 3. 원의 parametric equation.
만약 a 나 b 를 시간이 지남에 따라서 증가시키면, 원을 그릴 수 있다.
가능한 삼각함수 값의 법칙과 그래프.
가능한 삼각함수 값의 법칙을 이야기할 때 그래프를 그려 줬다면 더 이해하기 쉽지 않았을까 생각한다.

그림 4. sine 그래프. 출처 : Trigonometry. Wikipedia.

그림 5. tangent 그래프. 출처 : Trigonometry. Wikipedia.
여러 삼각함수들의 기하학적 관계.
여러 가지 삼각함수들의 기하학적 관계가 아래 그림에 나와 있다. 만약 모른다면 일일이 계산해야 할 것 같은데...
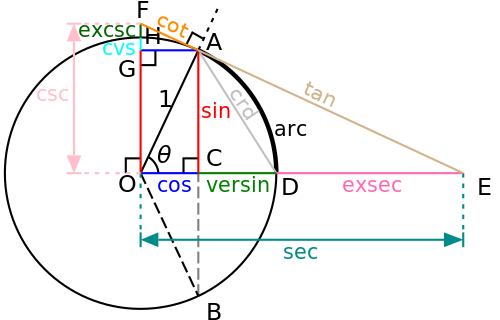
그림 6. 여러 삼각함수들의 관계. 출처 : Trigonometry. Wikipedia.
'물리_수학_기하학 > 이야기로 아주 쉽게 배우는 삼각함수' 카테고리의 다른 글
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 11. 극 좌표계 (0) | 2013.08.30 |
|---|---|
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 10. 삼각함수의 역함수 (0) | 2013.08.29 |
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 9. 파동 (0) | 2013.08.28 |
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 8. 삼각함수 그래프 (2) | 2013.08.26 |
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 7. 사인법칙과 코사인법칙 (0) | 2013.08.24 |
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 6. 삼각함수 항등식 (0) | 2013.08.22 |
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 4. 삼각함수의 응용. (0) | 2013.08.18 |
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 3. 삼각함수 : sin, cos, tan (0) | 2013.08.16 |
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 2. 직각삼각형 문제를 풀다. (0) | 2013.08.15 |
| [ 이야기로 아주 쉽게 배우는 삼각함수 ] 1. 각도와 삼각형. (0) | 2013.08.15 |


